Cycles all way down

A while ago while working on Rust-based Emacs, I was loading a new elisp file and hit a stack overflow. Digging deeper I found the issue in trying to print a cyclic list (where the tail of the list points back to previous element). I knew this was a possibility, and that at some point I would have to handle cycles.

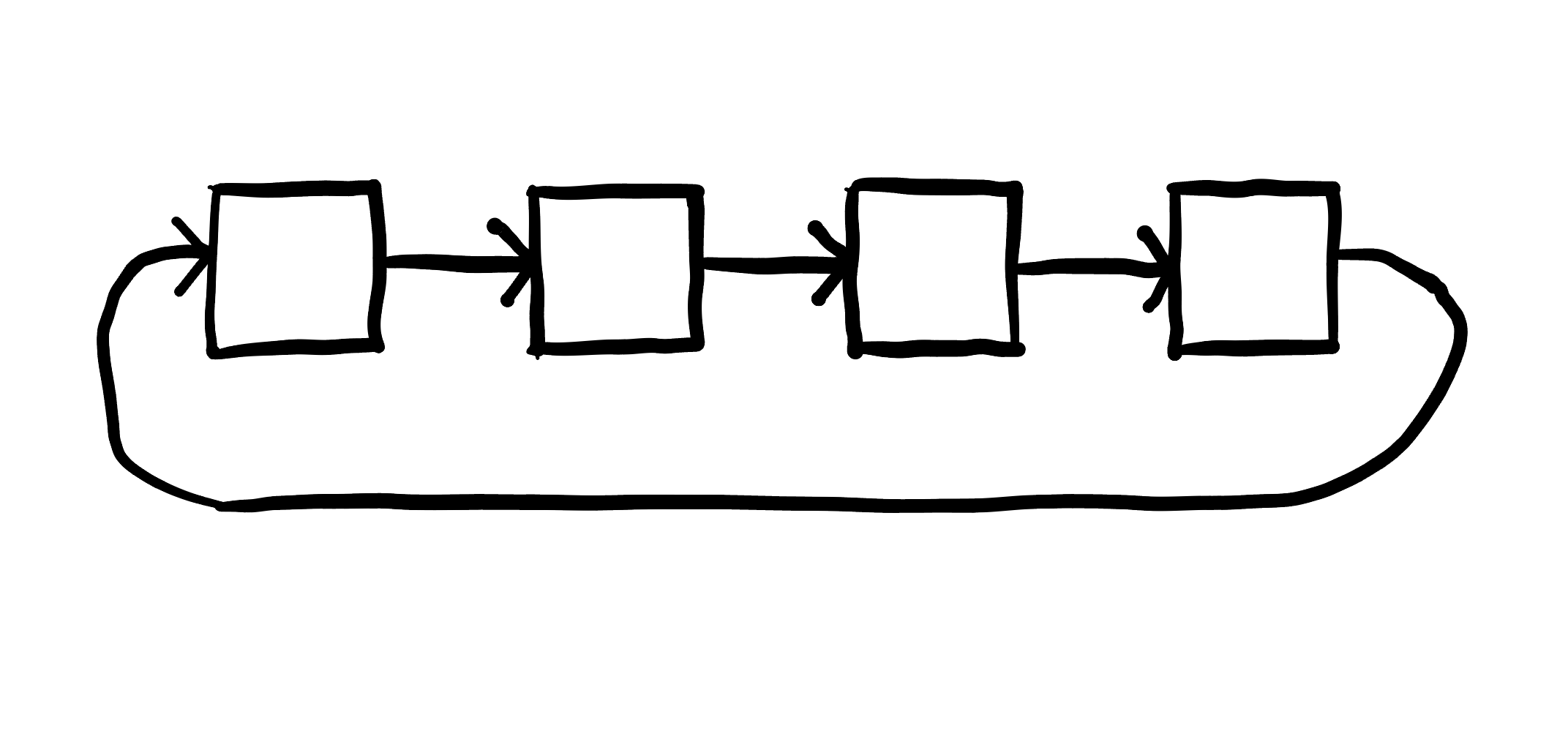
So I quickly implemented a version of Floyd’s cycle detection algorithm (visualized here). If you want to dive deeper into the algorithm use the links, but the high level is that you have a second pointer when traversing a list that moves two nodes for each node the main pointer moves. If there is a cycle, they will both meet at or before the first pointer has gone around the loop once. This is great because it is simple, and only has one additional pointer of overhead.

But the very next day I hit a stack overflow again. Digging in deeper it was a cycle again, but this time it was not a cycle at the end of the list but instead one of the elements contained another list and that list pointed back to the main one. So this was a cycle in the depth of the list instead of the length.

Cycle in length

Cycle in depth

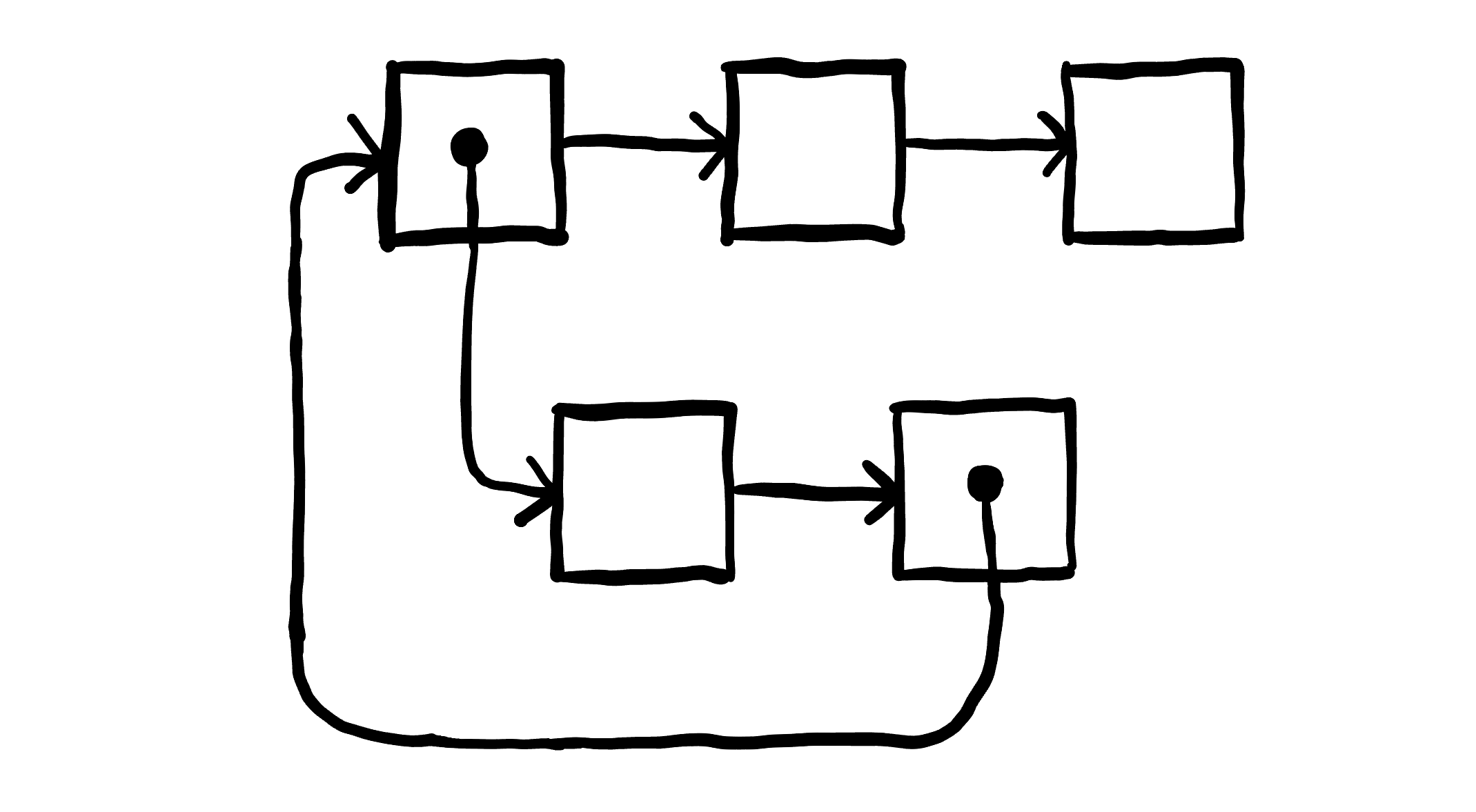
It was at this point that I realized that a lisp list can be viewed more like a tree than a linear list. Cycles can occur on any branch. No problem I thought, I am sure this has been solved before, I will just google the right algorithm and implement that. But I was not able to find what I was looking for. The best I could find was this DFS algorithm where you put every node in a hashmap and then check if each new node for backlinks. This was much heavier than the simple two pointer approach of Floyd’s. You now have linear memory usage and large (but constant time) overhead for each element¹.

What does Emacs do

At this point, I decided to go check the Emacs source code (which I should have done in the first place). My first surprise is that they are not using Floyd’s algorithm at all. Instead it uses Brent’s algorithm. This still uses two pointers, but instead of moving one at twice the speed of the other, it searches for the smallest power of two larger than the cycle. It will iterate the first pointer through all elements until it has moved a power-of-two, then it will move the second pointer to match the first and go to the next power of two. For example, if there is a loop of 12 elements, The algorithm will first move the pointer 2^1 (2) elements, then move it 2^2 (4) elements, 2^3 (8) elements, and finally 2^4 (16) elements. On the last loop, the first and second pointers will meet and the cycle will be found (because 16 is larger than the size of the cycle).

comparison

How does this compare to Floyd’s algorithm? Let’s look at the total number of comparisons and total number of elements visited.

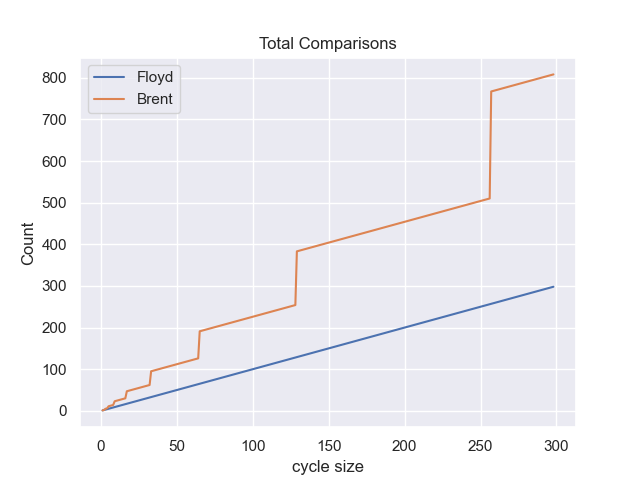
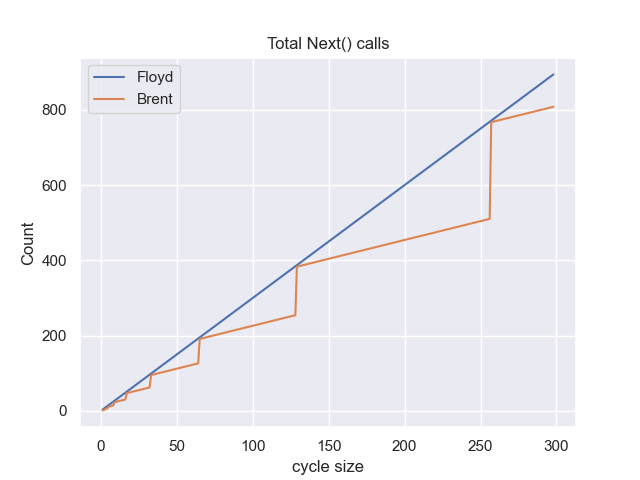
Brent’s power-of-two step function is clearly visible in the graph. You exchange a higher number of total comparisons for fewer calls to next (or cdr in lisp terms). Since comparisons are quite a bit cheaper than following a pointer (which could result in a cache miss), this is generally a win. You can see this step function in Emacs if you evaluate the following code:

(dotimes (n 32)
  (let (list)
    (dotimes (m (1+ n))
      (push (format "%02d" m) list))
    (setcdr (nthcdr (1- (length list)) list) list)
    (message "%s" list)))

This will print out the following output:

(00 . #0)
(01 00 01 00 . #2)
(02 01 00 02 01 . #2)
(03 02 01 00 03 02 01 00 03 02 . #6)
(04 03 02 01 00 04 03 02 01 00 04 . #6)
(05 04 03 02 01 00 05 04 03 02 01 00 . #6)
(06 05 04 03 02 01 00 06 05 04 03 02 01 . #6)
(07 06 05 04 03 02 01 00 07 06 05 04 03 02 01 00 07 06 05 04 03 02 . #14)
(08 07 06 05 04 03 02 01 00 08 07 06 05 04 03 02 01 00 08 07 06 05 04 . #14)
(09 08 07 06 05 04 03 02 01 00 09 08 07 06 05 04 03 02 01 00 09 08 07 06 . #14)
(10 09 08 07 06 05 04 03 02 01 00 10 09 08 07 06 05 04 03 02 01 00 10 09 08 . #14)
(11 10 09 08 07 06 05 04 03 02 01 00 11 10 09 08 07 06 05 04 03 02 01 00 11 10 . #14)
(12 11 10 09 08 07 06 05 04 03 02 01 00 12 11 10 09 08 07 06 05 04 03 02 01 00 12 . #14)
(13 12 11 10 09 08 07 06 05 04 03 02 01 00 13 12 11 10 09 08 07 06 05 04 03 02 01 00 . #14)
(14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 14 13 12 11 10 09 08 07 06 05 04 03 02 01 . #14)
(15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 15 14 13 12 11 10 09 08 07 06 05 04 03 02 . #30)
(16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 16 15 14 13 12 11 10 09 08 07 06 05 04 . #30)
(17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 17 16 15 14 13 12 11 10 09 08 07 06 . #30)
(18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 18 17 16 15 14 13 12 11 10 09 08 . #30)
(19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 19 18 17 16 15 14 13 12 11 10 . #30)
(20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 20 19 18 17 16 15 14 13 12 . #30)
(21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 21 20 19 18 17 16 15 14 . #30)
(22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 22 21 20 19 18 17 16 . #30)
(23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 23 22 21 20 19 18 . #30)
(24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 24 23 22 21 20 . #30)
(25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 25 24 23 22 . #30)
(26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 26 25 24 . #30)
(27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 27 26 . #30)
(28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 28 . #30)
(29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 . #30)
(30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 . #30)
(31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 09 08 07 06 05 04 03 02 . #62)

Looks like the graph above turned on its side! Notice how Emacs will print the elements of the list 2-3 times before it finds the cycle. Floyd’s will only print them once, but the fast pointer will traverse them an additional 2 times, for a total of 3 traversals for each element. That will only happen in Brent’s if the loop is a (2^N)+1 node.

Cycle detection in depth

But Brent’s algorithm has the same weakness as Floyd’s in that it can only detect cycles in the tail of a list. So how does Emacs handle cycles in depth? It turns out by combining it with the DFS algorithm we found on StackOverflow!

As it goes down the structure it pushes nodes on a being_printed stack. As it does, it checks if the current node is in the stack. If it is then we have found a cycle. When we are done with a particular “level” those elements are popped from the stack (by decrementing the print_depth index). This works because there can only be a cycle if some node points back to a previous node along that same path. The code is fairly simple:

for (int i = 0; i < print_depth; i++)
  if (BASE_EQ (obj, being_printed[i]))
    {
      int len = sprintf (buf, "#%d", i);
      strout (buf, len, len, printcharfun);
      goto next_obj;
    }
being_printed[print_depth] = obj;

In Emacs, this stack is set to a hard limit of 200 elements. Meaning that if you have a structure that is deeper than that, it will error out. We can see this in the code below.

(let* ((x (cons nil 0))
       (head x))
  (dotimes (n 200)
    (let ((next (cons nil n)))
      (setcar x next)
      (setq x next)))
  (prin1-to-string head))

This will throw the error “Apparently circular structure being printed”. You can work around this by enabling print-circles, which will store all the nodes in a hashtable so it can properly print cycles in a way that can be read back in.

I think this is a clever solution! It combines the speed and simplicity of Brent’s algorithm with the DFS. Since most structures in lisp tend to be “longer” than they are “deep” this is a good trade-off. I decided to write about this because I could not find this particular solution on the Internet and most of the things I did find were very high-level and generic. I like this solution as a combination of engineering and science.

Have a comment?

Join the discussion or send me an email.