Text showdown: Gap Buffers vs Ropes

I have been working on a hobby project to reimagine the C core of Emacs in Rust. On this journey, I reached the point where I needed some way to represent the text of a buffer. The simplest approach is to just use a large string or array of lines. However these each suffer from poor performance as either the size or line length of text increases.

GNU Emacs has famously used a gap buffer to represent editable text. It’s even mentioned by name on the wikipedia entry for it. Gap buffers have the advantage of allowing fast local edits with a fairly simple design. Essentially you hold the text in a giant array with a gap of unused bytes in the middle. When you insert text, you replace some of the bytes with text, making the gap smaller. When you want to insert somewhere else in the text, you move the gap to that location and do the same operation. Delete performs the opposite operation, expanding the gap. With this simple mechanism, you can efficiently represent editable text.

I see it as analogous to the more general data structure, the “array”. A gap buffer is just an array that is optimized for inserting at a “cursor” instead of at the end. Using a gap buffer has served Emacs well over many decades.

Despite this, Emacs seems largely alone in its choice in the modern world. Most popular editors today use some variation of either a piece table or a rope. Rather than storing data as a large contiguous array, these data structures chop the buffer into small chunks and operate on those. This enables them to avoid the O(n) penalty of moving the cursor when doing edits far away and the latency of resizing the buffer.

Rust has many rope crates that have had a lot of optimization work put in. The obvious thing to do was to just pick one and move on. But I wanted to see for myself how the gap buffer holds up to these more “advanced” data structures. Modern computers can operate very quickly over linear memory. So I built a gap buffer and stacked it up against the competition.

Design

My gap buffer (link) is fairly true to the original design, with one big change; I store metrics about the buffer in a separate tree. These metrics include things like char and line position, but could, in theory, include anything you want (like UTF-16 code units). This means that finding an arbitrary position in the buffer becomes at worse O(logn), but we still have to pay the cost of moving the gap.

The ropes that I will be comparing against are Ropey, Crop, and Jumprope. The last one is technically implemented via skip lists, but that’s an implementation detail and the performance should be similar.

Gap buffer costs

Before we jump into benchmarks comparing ropes and gap buffers. Let’s look at the time it takes to complete the two highest latency operations on gap buffers: resizing and moving the gap. This is a cost that ropes don’t share because their worst case for an editing operation is O(logn).

Resize

Insertion in a gap buffer is O(1), just like an appending to a vector. But also like vectors, they only achieve this in the amortized case. Vectors need to resize once they get full, and this is a O(N) operation. But since the time between resizing is N appends, it averages out to O(1). Gap buffers are similar, except that we don’t usually continue to grow the gap as the text gets larger (that would lead to more overhead). In this sense, it isn’t truly O(1) insertion time, but even if it was, we generally care about the latency in interactive applications more than we care about the average case.

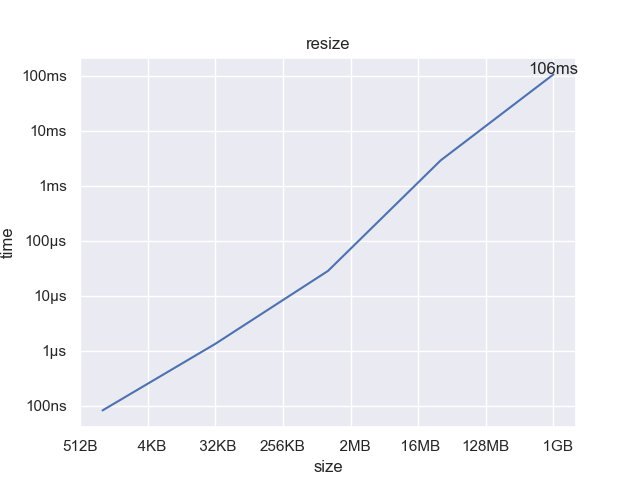
Note that both axes are logarithmic. We can see that the cost to resize grows linearly with the size of the buffer, which is what we would expect. With a 1GB¹ file, it takes a little over 100ms to resize, which is starting to be perceptible.

Moving the gap

How long does it take to slide the gap a given distance? This delay is added anytime we edit a different part of the buffer than we are currently in. The farther the move, the longer it takes. Unlike resizing which (from a user’s perspective) strikes randomly, this latency is easier to predict. You generally know when you are editing something farther than where you are currently at.

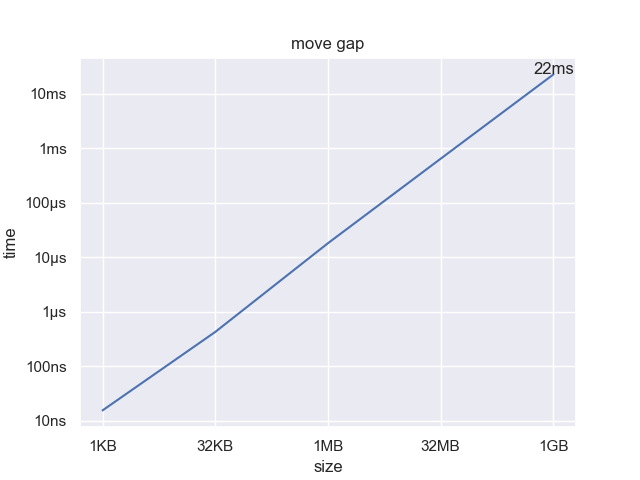
Moving the gap 1GB is significantly faster than resizing 1GB, taking only 22ms. This isn’t nothing, but is small enough to be imperceptible. Of course, since this is a O(n) relationship, moving the gap even farther will have a proportionally higher cost.

In practice, these latencies will be less of an issue, because giant files tend to be log files and auto-generated output, which are rarely edited. However, it is still an unavoidable cost of storing data in a contiguous fixed-sized structure.

Memory overhead

For our comparisons, let’s start with memory overhead. The way to read this is if something has 50% overhead, that means you need 1.5GB of memory to open a 1GB file.

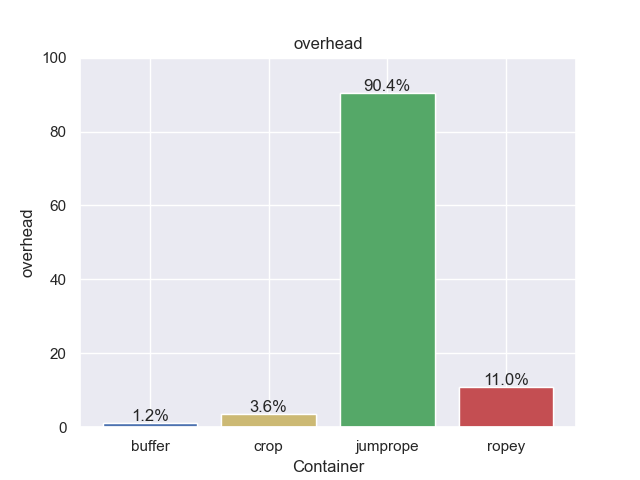
Woah! Jumprope is way outside the norm here, almost doubling the memory needed to open a file². Crop and Ropey are much closer to what you would expect. However, this is the ideal case of opening a new file. Each rope node will be perfectly filled and the tree properly balanced.

Edit overhead

Let’s look at the overhead when edits are applied to the text. These could be things like large search and replace or multiple cursors. This tends to leave the ropes in a less ideal state, and hence have higher overhead.

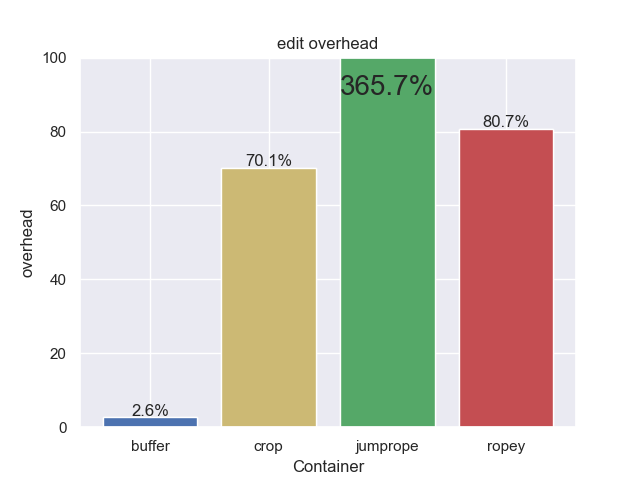
Fairly significant change for all ropes. Jumprope has gone through the roof, jumping so high that I didn’t even bother expanding the plot to show it. Even crop, which had the lowest rope overhead in ideal conditions, has jumped almost 20x. The gap buffer on the other hand has barely moved. Unlike ropes, a gap buffer is always in ideal state with regards to layout. This unique property will show up later in the searching benchmarks.

Real world

To compare editing performance we have a set of 5 real world benchmarks from the author of Jumprope. These are recordings or “traces” of actual people editing some text in an editor. Each benchmark starts empty, then replays thousands of edits and arrives at the end text.

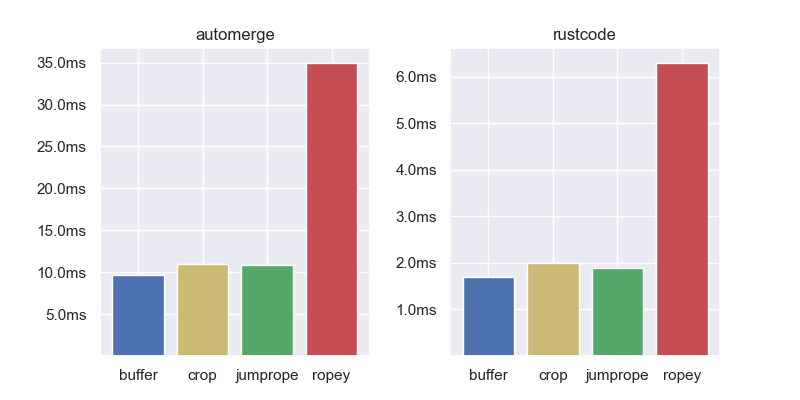
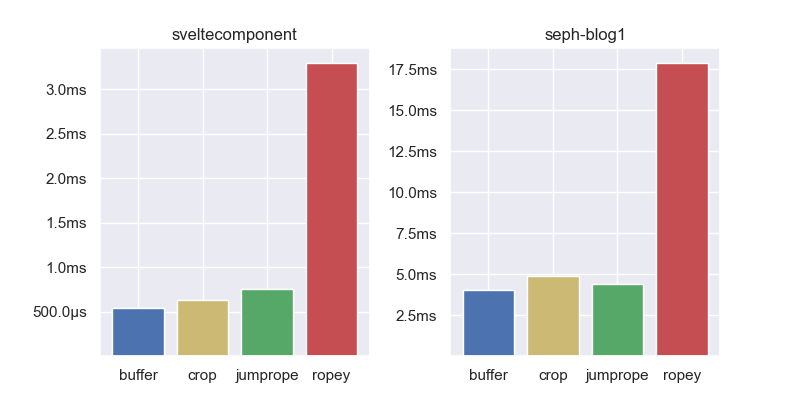
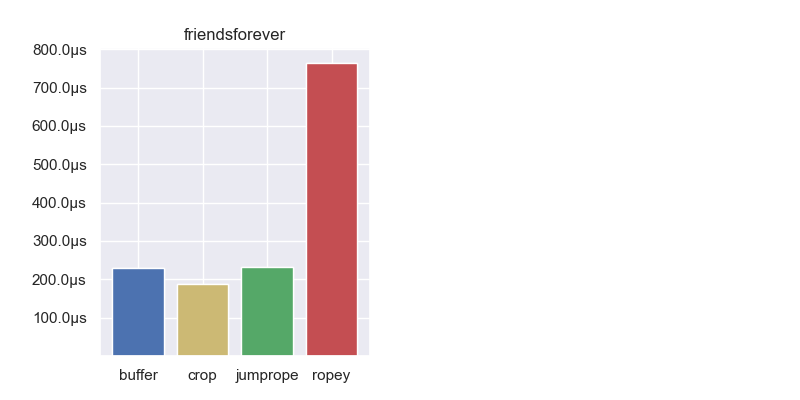
Aside from Ropey, all the containers have comparable performance. In all benchmarks but one, the gap buffer is the fastest, but not by any meaningful amount. This demonstrates that in the average case, insert and delete performance is fairly comparable between the different data structures. Let’s zoom in on some specialized use cases.

Creating

So we have a sense of the memory overhead and average performance for the different containers. Here we will compare the time to load and save the text from the data structures.

Creating from a String

How long does it take to create a new data structure from a String? The string below is 1GB in size.

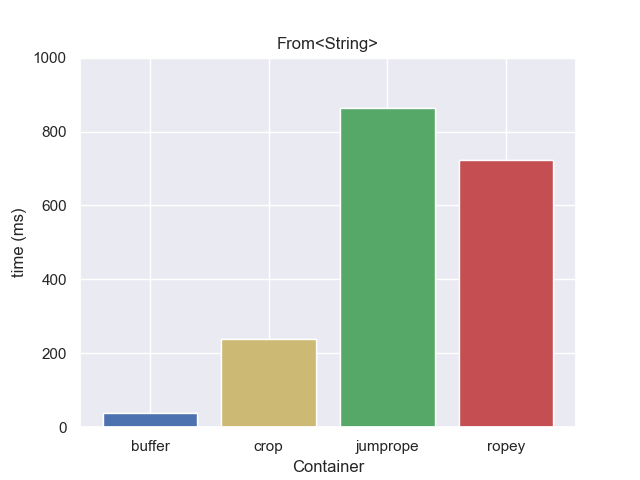
The gap buffer is significantly faster than the rest, but it’s not really a fair comparison. A String is essentially already a gap buffer. It has the string text, followed by some amount of unused capacity which can be used as a gap. So in this case we don’t need to copy or allocate at all, instead reusing the allocation from the string. That won’t always be the case, so how do things compare if we force them all to copy the source text? This would be the case when loading from a file.

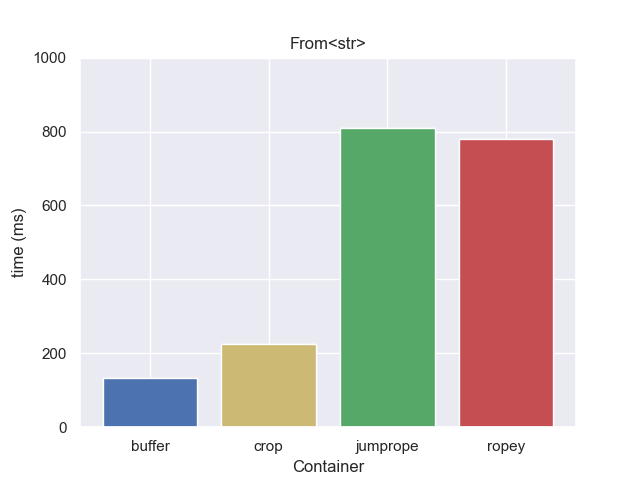
Forcing a copy makes the gap buffer take about three times as long, but it is still faster than the rope implementations.

Saving

What about saving a file? Here we are not going to benchmark the actual file system overhead, but instead use “writing the contents of 1GB to a string” as a proxy.

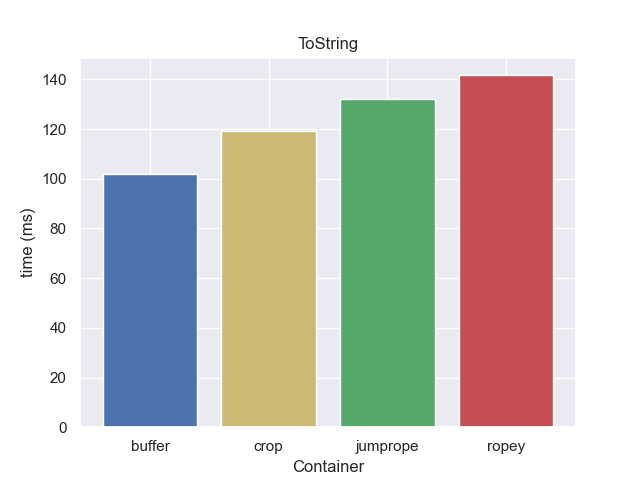
All containers are pretty comparable on this front.

Multiple cursors

Back in 2017, Chris Wellons wrote a blog post titled “Gap Buffers Are Not Optimized for Multiple Cursors”. It makes the case that since gap buffers have to move the gap buffer back to the first cursor for each edit (a O(n) operation), they don’t scale well with multiple cursors. So instead of using multiple cursors, you should use some other editing operation like macros. This idea has now become part of Internet lore.

I was not convinced by this argument. For one thing, there are no benchmarks, and many things that make sense intuitively don’t play out that way in the real world. Also, I realized you can avoid the overhead of moving the gap back to the first cursor with this one weird trick (computer scientists hate him!): Every time you do an edit, you reverse the direction you iterate through the cursors. If in one edit you go from the first cursor to the last, then in the next edit you go from the last cursor to the first. This saves the overhead of moving the gap back to the first cursor each time. Essentially you just sweep the gap back and forth as you make edits. Let’s benchmark this and see how well it works.

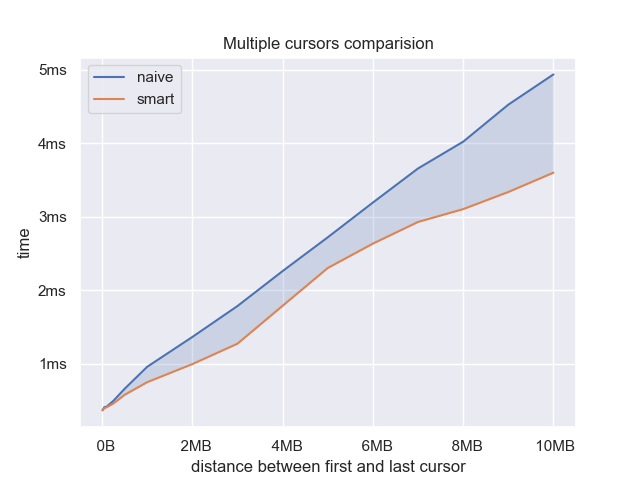
It looks like this trick works. Let’s zoom in on the percent overhead of the naive version.

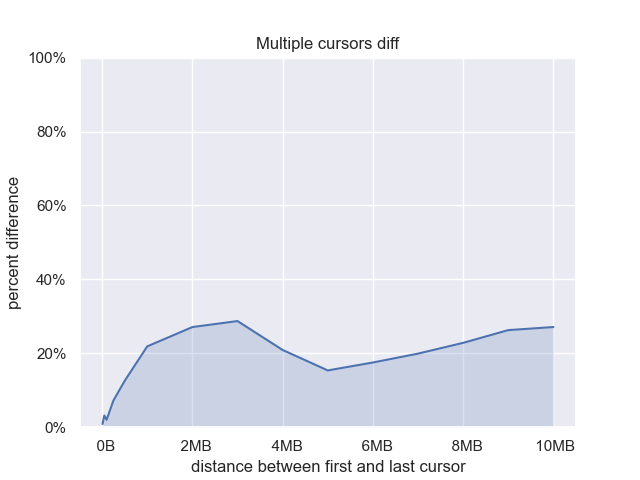
Once the distance gets large enough we have about 20-30% overhead. This shows that even in the naive case, most of the time is dominated by performing the actual edits, not moving the cursor back. Also, The overhead doesn’t grow linearly with the distance between the cursors.

Compared to ropes

How does this compare to the rope implementations? We will start with cursors 100 bytes apart and increase the total cursor count.

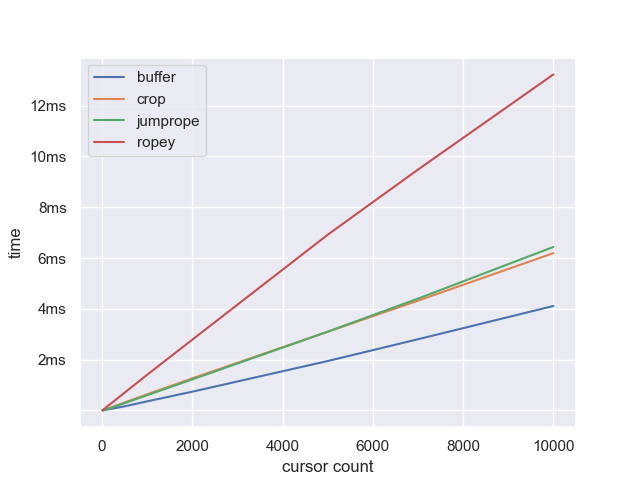
The relationship is almost perfectly linear, with Crop and Jumprope about twice as fast as Ropey but 50% slower than the gap buffer. This relationship continues as we move beyond 10,000 cursors. So having high numbers of cursors doesn’t impact gap buffers.

But one thing that might cause trouble is the distance between the cursors. Let’s benchmark 100 cursors while varying the average distance between them:

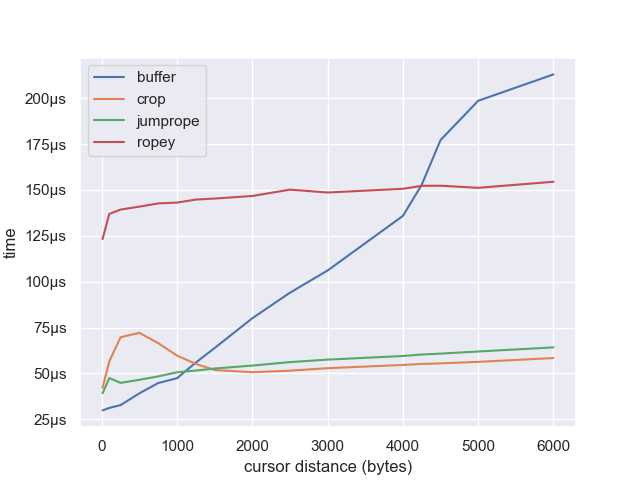
Now the weakness of gap buffers starts to show. The distance between cursors does not matter to ropes, because every edit is O(logn), however, it matters a lot to gap buffers. You can see that the ropes are all roughly flat, but the gap buffer has a positive slope. After about 1K Jumprope and Crop start to beat it, and after about 4K it falls behind Ropey.

However, there is nothing special about multiple cursors with this relationship. Gap buffers struggle with long-distance edits no matter what mechanism is used. It would be the same with macros, search and replace, etc. Given that, I would claim that gap buffers are optimized for multiple cursors just fine, it is non-local edits that are the source of the issue.

Searching

People don’t only edit text, they also analyze it. One of the most common ways to do this is via searching. Rust has a highly optimized regex crate, but it only operates on slices. This is problematic for ropes since they store the buffer in many small allocations. Currently, the best way to do a regex search over a rope is to copy all the chunks out into a separate allocation and perform your search over that³. There is some work to create a streaming API version of regex based on regex-automata, but it still has not been developed and may never prove to be as fast as slice searching.

EDIT 4/1/2024: The regex-cursor crate (an implementation of regex streaming) is finished and is being used in Helix. Overall the performance is quite good, but there are some areas where it is an order of magnitude slower than Regex. However these will improve over time. I have added the ropey-cursor benchmark to the plots below. It is within a factor of 2 of the gap buffer, which is huge improvement! But note that this is best case scenario for ropey-cursor since the regex used can be converted into a simple substring search (no-backtracking) and the rope is in ideal state (there have been no edits).

Given that, I wanted to test out how the different containers do when performing a full-text search. We would expect the gap buffer to have a significant advantage here because it is already in slice format.

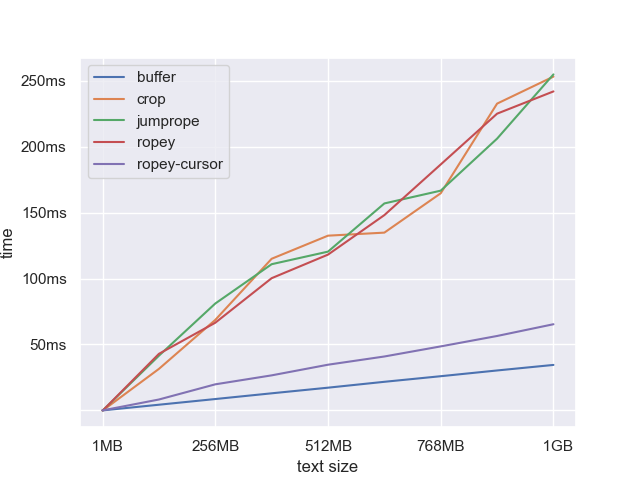
We can see that the buffer is a near-perfect line because we are essentially only benchmarking the speed of the regex engine. The ropes on the other hand have significantly higher overhead and more variability. Searching 1 GB text, the gap buffer runs in 35ms, which is around 7x faster than the next fastest rope (~250ms).

You might object that we are making things too easy for the gap buffer because the gap is at the start. If the gap was anywhere else we would need to move to before searching. Fair enough, but most of the time we wouldn’t need to move the gap all the way to the beginning or end. If the search is not multi-line, then you just need to move the gap to the nearest line boundary. But for the sake of analysis, let’s pretend we are doing a multi-line search. We will run the benchmark again with the gap in the middle of the text; the worst-case scenario. This will mean we need to move the gap 50% of the way across the text before we can begin searching.

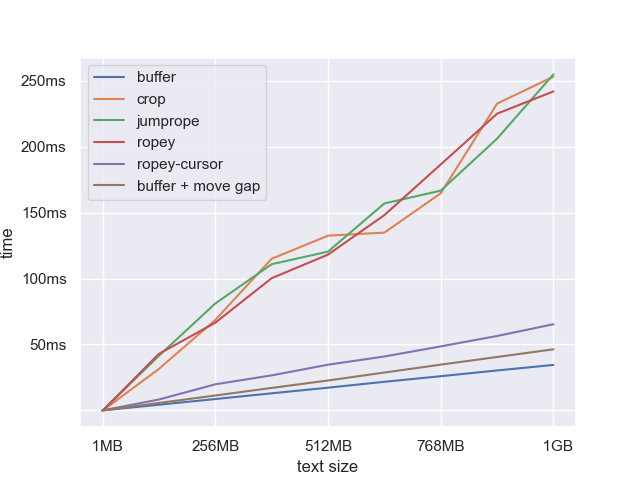
It adds about 30% overhead to the gap search. This still doesn’t put it anywhere near the ropes. Ultimately, the speed of search was one of the reasons that I chose gap buffer over ropes for my project. Emacs does a lot of searching.

That being said, many new parser libraries like Tree-sitter are already designed to operate on non-contiguous chunks, so the need for search becomes less important. We will see how this plays out in the future.

What should you use?

So is this to say that everyone should switch over and start using gap buffers? Not quite. Ropes are really powerful data structures, and they never have the latency spikes associated with resizing or moving the gap. In real-world editing scenarios it isn’t the best case or even the average case, it’s the worst-case tail latency that really matters. With ropes, you get worse case O(logn) behavior for all editing operations. As files get larger the extra latency associated with gap buffers starts to show itself. On the flip side, in my experience the larger a file is the less likely I am to be editing it, but the more likely I am to be searching it. These trade-offs work well in favor of gap buffers.

Ropes have other benefits besides good performance. Both Crop and Ropey support concurrent access from multiple threads. This lets you take snapshots to do asynchronous saves, backups, or multi-user edits. This isn’t something you could easily do with a gap buffer.

Despite all that, gap buffers showed they can do quite well when placed against more “advanced” data structures. One of their key advantages is that gap buffers are always in an ideal state. They never need to worry about fragmentation or being unbalanced like trees do. The way I see it, gap buffers are better for searching and memory usage, but ropes are better at non-local editing patterns. Despite their simplicity, gap buffers can hold their own in the modern world. Maybe Emacs was on to something.

Have a comment?

Join the discussion or send me an email. Benchmarks can be found here.